RNN和语言模型

Overview

学习新的NLP任务：语言模型
新的NN：RNN

语言模型

定义：一种预测下一个词是什么的NLP任务
数学表示：
$P(x^{t+1}=w_j|x^t,...,x^1)$
应用：输入法提示、搜索提示

BoW 词袋模型

就是统计每一个词出现的次数

from nltk.corpus import reuters
from collections import Counter
import random

counts = Counter(reuters.words())
total_count = len(reuters.words())

# Compute the frequencies
for word in counts:
    counts[word] /= float(total_count)

# Generate 100 words of language
text = []

for _ in range(100):
    r = random.random()
    accumulator = .0

    for word, freq in counts.iteritems():
        accumulator += freq

        if accumulator >= r:
            text.append(word)
            break

print ' '.join(text)

运行结果如下

1
2
3

[(u'.', 94687), (u',', 72360), (u'the', 58251), (u'of', 35979), (u'to', 34035), (u'in', 26478), (u'said', 25224), (u'and', 25043), (u'a', 23492), (u'mln', 18037), (u'vs', 14120), (u'-', 13705), (u'for', 12785), (u'dlrs', 11730), (u"'", 11272), (u'The', 10968), (u'000', 10277), (u'1', 9977), (u's', 9298), (u'pct', 9093)]
1.0
held pct said is A 1986 . qtr of A oil will non revenues rate said 2 lt already net They subsidiary compared have were FORECAST net 109 being the cts to cuts , and more Government said CASH SEES in Middle in of 732 SHIPPING some to of 03 , national they and / released and to , > Walker > said stages 1 would its agricultural the 1986 contract February STAKE Gencorp ; Savings > share ; 3 annual VENTURE Trade given dlrs had ago . be Albion be on from said OF . 1985 area the over

从结果可以看出，结果只是根据词频生成的

n-gram 语言模型

为了更好的生成文本，一个改进的想法就是考虑上下文信息
定义： n-gram 就是一组词，每组词是连续的，数量为$n$
思路：基于统计的方法，根据每组词出现的频率来预测下一个词
前提假设：$x^{t+1}$ 只依赖于它前面 $(n-1)$ 个词

math

$n-gram$ 和 $(n-1)-gram$ 的概率可由频率近似替代（统计）

优缺点

$n-gram$ 模型的优点包含了前 $(n-1)$ 个词所能提供的全部信息，这些信息对当前词出现具有很强的约束力。同时因为只看 $(n-1)$ 个词而不是所有词也使得模型的效率较高。

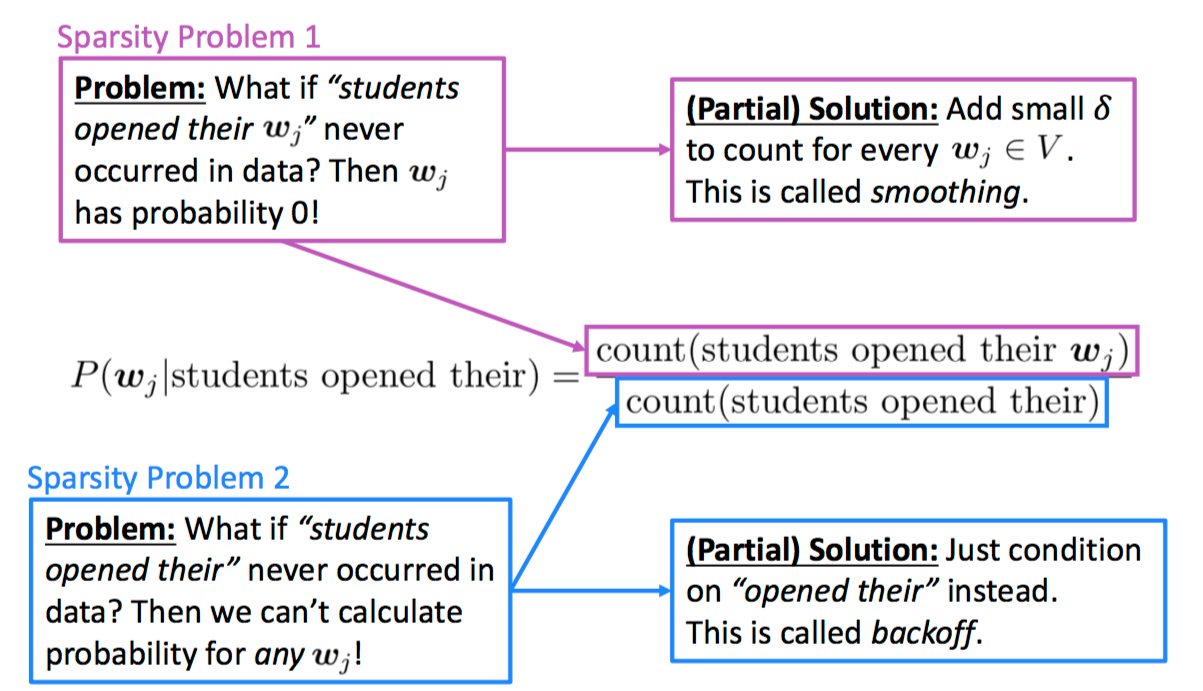
训练语料里面有些 n 元组没有出现过，其对应的条件概率就是 0，导致计算一整句话的概率为 0。解决这个问题有两种常用方法：

(1)方法一为平滑法。最简单的方法是把每个 $n$ 元组的出现次数加 1，那么原来出现 $k$ 次的某个 $n$ 元组就会记为 $k+1$ 次，原来出现 $0$ 次的 $n$ 元组就会记为出现 $1$ 次。这种也称为 $Laplace$ 平滑。当然还有很多更复杂的其他平滑方法，其本质都是将模型变为贝叶斯模型，通过引入先验分布打破似然一统天下的局面。而引入先验方法的不同也就产生了很多不同的平滑方法。

(2)方法二是回退法。有点像决策树中的后剪枝方法，即如果 $n$ 元的概率不到，那就往上回退一步，用 $n-1$ 元的概率乘上一个权重来模拟。

from nltk.corpus import reuters
from nltk import bigrams, trigrams
from collections import Counter, defaultdict
import random

model = defaultdict(lambda: defaultdict(lambda: 0))
for sentence in reuters.sents():
    for w1, w2, w3 in trigrams(sentence, pad_right=True, pad_left=True):
        model[(w1, w2)][w3] += 1

for w1_w2 in model:
    total_count = float(sum(model[w1_w2].values()))
    for w3 in model[w1_w2]:
        model[w1_w2][w3] /= total_count



text = [None, None]
sentence_finished = False

while not sentence_finished:
    r = random.random()
    accumulator = .0

    for word in model[tuple(text[-2:])].keys():
        accumulator += model[tuple(text[-2:])][word]

        if accumulator >= r:
            text.append(word)
            break

    if text[-2:] == [None, None]:
        sentence_finished = True


# add the probability computation
text = [None, None]
prob = 1.0  # <- Init probability

sentence_finished = False

while not sentence_finished:
    r = random.random()
    accumulator = .0

    for word in model[tuple(text[-2:])].keys():
        accumulator += model[tuple(text[-2:])][word]

        if accumulator >= r:
            prob *= model[tuple(text[-2:])][word]  # <- Update the probability with the conditional probability of the new word
            text.append(word)
            break

    if text[-2:] == [None, None]:
        sentence_finished = True

测试一下：

1 2	print "Probability of text=", prob # <- Print the probability of the text print ' '.join([t for t in text if t])

Probability of text= 1.82814299952e-05
He told a press conference .

神经语言模型

A fixed-window neural Language Model

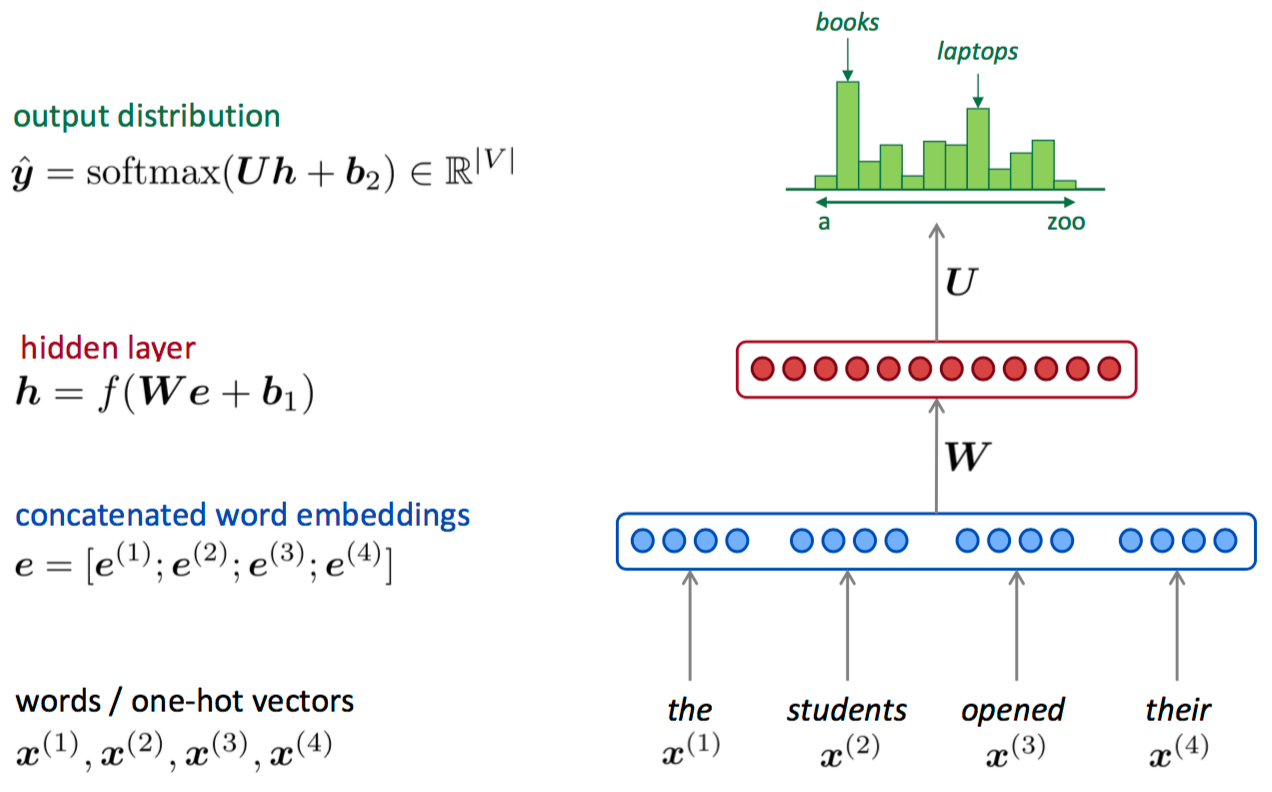
neural

优点

词表示不再是稀疏的；模型复杂度从 $O(exp(n))$ 降低为 $O(n)$

缺点

窗口太小，但如果增大窗口 $W$ 也随之变大，而且窗口中每一个词 $x^{(i)}$ 使用的是 $W$ 中不同的行，也就是说 $W$ 不能共享

为了能重复的使用 $W$，提出了 $RNN$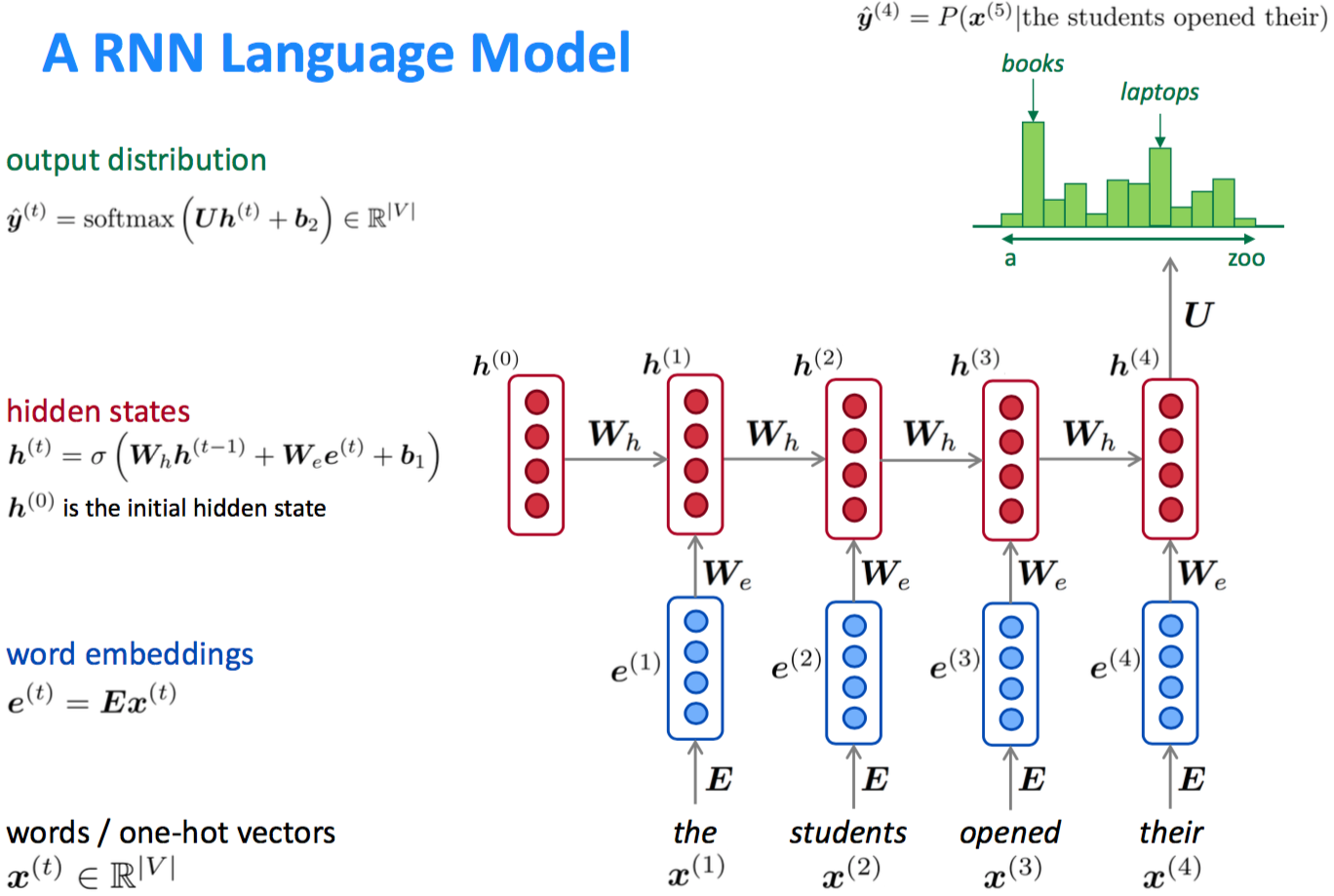

优点

（1）输入可以是任意长度的

（2）模型规模不会随输入长度变化而变化

（3）“记忆能力”：当前时刻的计算使用过去的信息

（4）不同时刻的权重是共享的，即表示是共享的

缺点

（1）递归使得计算过程很慢

（2）记忆能力也是有限的

RNN 简介

递归神经网络（Recurrent Neural Networks，RNN）是两种人工神经网络的总称：时间递归神经网络（recurrent neural network）和结构递归神经网络（recursive neural network）。时间递归神经网络的神经元间连接构成有向图，而结构递归神经网络利用相似的神经网络结构递归构造更为复杂的深度网络。

RNN一般指代时间递归神经网络。单纯递归神经网络因为无法处理随着递归，权重指数级爆炸或消失的问题（Vanishing gradient problem），难以捕捉长期时间关联；而结合不同的LSTM可以很好解决这个问题。时间递归神经网络可以描述动态时间行为，因为和前馈神经网络（feedforward neural network）接受较特定结构的输入不同，RNN将状态在自身网络中循环传递，因此可以接受更广泛的时间序列结构输入。

HMM

RNN主要解决序列数据的处理，比如文本、语音、视频等等。这类数据的样本间存在顺序关系，每个样本和它之前的样本存在关联。比如说，在文本中，一个词和它前面的词是有关联的；在气象数据中，一天的气温和前几天的气温是有关联的。一组观察数据定义为一个序列，从分布中可以观察出多个序列。
隐马尔科夫模型（HMM）定义每个元素只和离它最近的$k$个元素相关，解决了复杂度暴增的问题.只考虑观察值$X$的模型有时表现力不足，因此需要加入隐变量，将观察值建模成由隐变量所生成。隐变量的好处在于，它的数量可以比观察值多，取值范围可以比观察值更广，能够更好的表达有限的观察值背后的复杂分布。加入了隐变量$h$的马尔科夫模型称为隐马尔科夫模型。隐马尔科夫模型实际上建模的是观察值$X$，隐变量$h$和模型参数 $\theta$ 的联合分布,HMM的模型长度$T$是事先固定的，模型参数不共享，其复杂度为 $O(T)$。

RNN

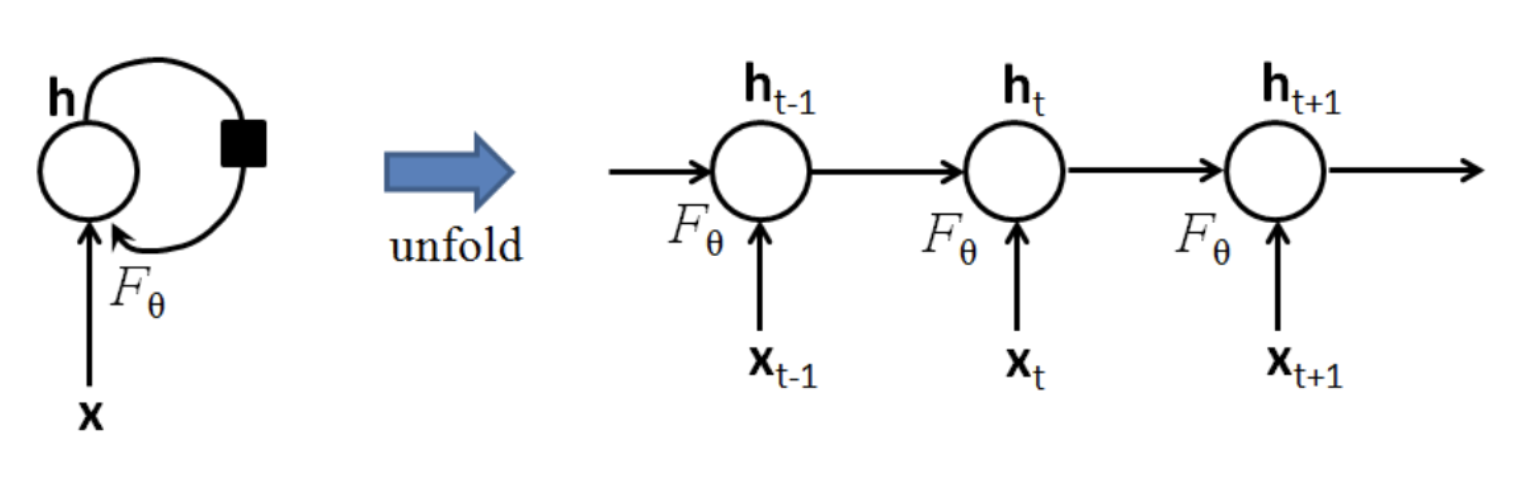
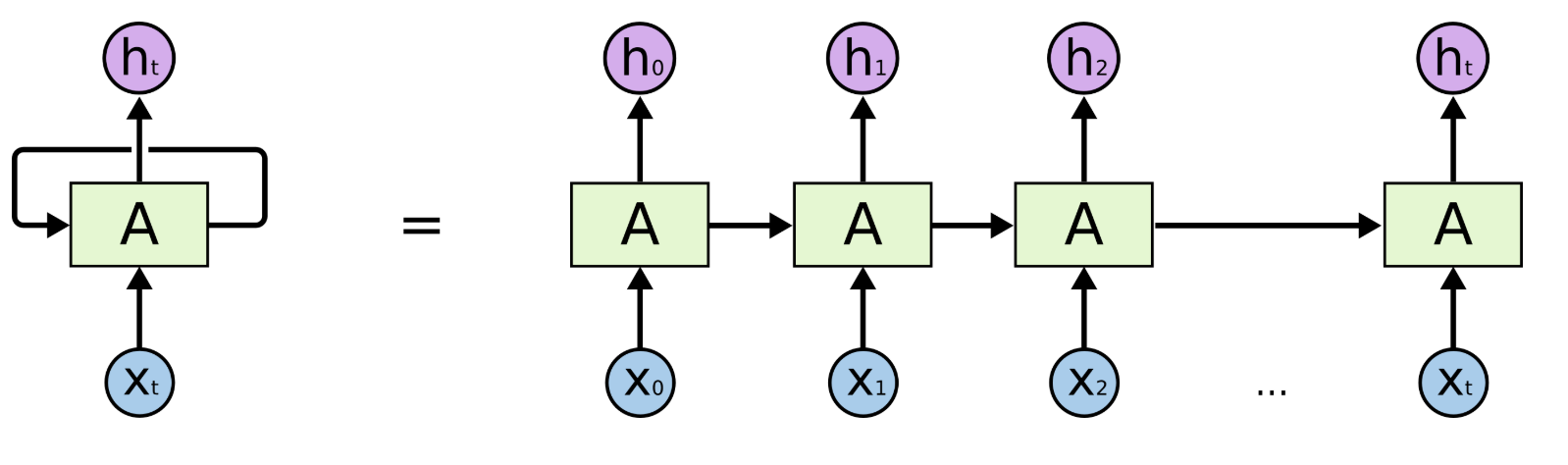
把序列视作时间序列，隐含层 $h$ 的自连接边实际上是和上一时刻的 $h$ 相连（上面左图）。在每一个时刻$t$，$h_t$ 的取值是当前时刻的输入 $x_t$ 和上一时刻的隐含层值 $h_{t-1}$ 的一个函数.

$h_t=F_{\theta}(h_{t-1}, x_t)$

将 $h$ 层的自连接展开，就成为了上图右边的样子，看上去和HMM很像。两者最大的区别在于，RNN的参数是跨时刻共享的。也就是说，对任意时刻 $t$ ，$h_{t-1}$ 到 $h_{t}$ 以及 $x_{t-1}$ 到 $h_{t}$ 的网络参数都是相同的。

训练 RNN-LM 的相关细节

在一组句子中的每个句子上而不是整个 corpus 上计算 loss 和 gradient
$J^{(t)}(\theta)$ 对权重矩阵 $W_h$ 的偏导，等于 $J^{(t)}(\theta)$ 对每个权重值 $w_i$ 的偏导的加和。
多变量的链式法则
反向传播：backpropagation through time
评价指标: 困惑度（一种信息论度量，用来测量一个一个概率模型预测样本的好坏，困惑度越低越好）

给定一个包含 $n$ 个词的文本语料 $w_1,…w_n$ 和一个基于词语历史的用于为此与分配概率的语言模型函数 $LM$ , $LM$ 在这个语料的困惑度是

$2^{- \frac{1}{n} \sum_{i=1}^nlog_2LM(w_i|w_{1:i-1})}$

Tips

困惑度与预料有关
困惑度适用于比对不同的语言模型，因为他有能力学会序列中的规律，但他不是一个很好的用于去评估语言理解或者语言处理任务的度量