这节课介绍了根据上下文预测单词分类的问题，与常见神经网络课程套路不同，以间隔最大化为目标函数，推导了对权值矩阵和词向量的梯度；初步展示了与传统机器学习方法不一样的风格。

前期知识准备

softmax 复习

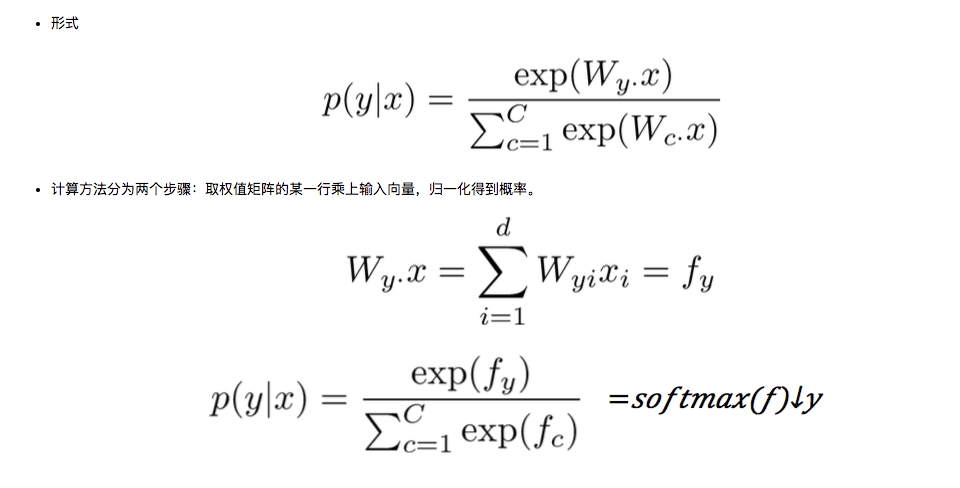
softmax与交叉熵

用 softmax 分类时，常用交叉熵作为损失函数(目标函数)。
训练的时候，可以直接最小化正确类别的概率的负对数：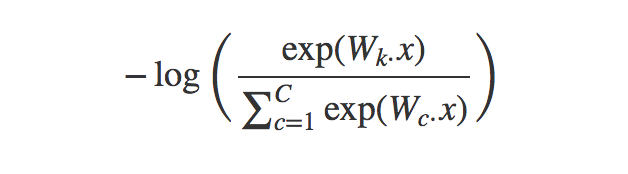

其实这个损失函数等效于交叉熵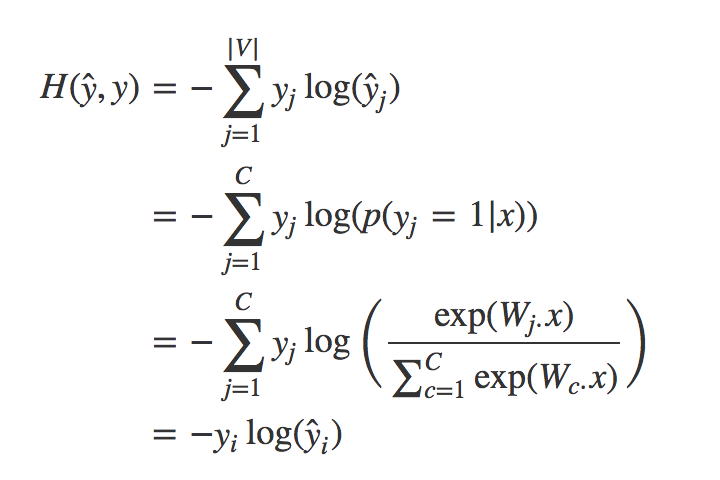

这是因为类别是one-hot向量。

下面补充说明熵、KL散度、损失函数的一些问题

如何衡量真实概率和预测概率之间的差异
熵：可以表示一个事件A的自信息量，也就是A包含多少信息
$S(A)=-\sum_i P_A(x_i) log P_A(x_i)$
KL散度：可以用来表示从事件A的角度出发，事件B有多大不同

$D_{KL}(A||B) = \sum_i P_A log(\frac {P_A(x_i)}{P_B(x_i)}) = \sum_i P_A(x_i) log(P_A(x_i))-\sum_i P_A(x_i) log(P_B(x_i))$

交叉熵：可以用来表示从事件A的角度出发，如何描述事件B

$H(A, B)=- \sum_i P(x_i)log(P_B(x_i))$ $D_{KL}(A||B) = -S(A + H(A, B)$

KL散度可以被用于计算代价，而在特定的情况下，min(KL) <=> min(cross_entropy). 而交叉熵的运算更简单，所以用交叉熵来做代价函数

模型学到的分布 $P(model)$

训练数据的分布 $P(train)$

真实数据的分布 $P(real)$

为什么交叉熵可以作为代价？

$P(model)$ ~ $P(train)$ => $KL(P(train)||P(model))$

此处 $P(train)$ 就是事件A， $P(model)$ 就是事件B

恰好，训练数据的分布是给定的、已知的，所以求 $D_{KL}(A||B)$ <=> 求 $H(A, B)$

Window Based NER

这是一种根据上下文给单个单词分类的任务，可以用于消歧或命名实体分类。

“Spokesperson for Levis, Bill Murray, said . . . ”
where it is ambiguous whether Levis is a person or an organization.
“Heartbreak is a new virus,” where “Heartbreak” could either be a MISC named entity
(it’s actually the name of a virus), or simply a noun.

Basically, we are looking for any situation wherein the sentence contains a word

softmax classifier & cross_entropy loss

训练了一个softmax 分类器，其中 x 是一个窗口中中心词+上下文的向量拼接，y 是中心词的类别，仍然使用交叉验证熵作为我们的损失函数

这里 $C$ 指的是多类别的类别数，$W$ 是一个 $C\times d$ 的矩阵，$d$ 指的是向量 $X_{window}$ 的维度，注意这里 $X_{window}$ 是把 5 个单词的词向量 contact 了起来，如图所示
是一个 $(5\times 4)\times 1=20\times 1$ 的向量。$W_y$ 指的是 $W$ 第 $y$ 行的向量，$J(\theta)$ 中的参数 $\theta$ 便
是 $W$ 中的各个元素。我们的目标便是最小化这个损失函数。

但是一个广义线性的模型，不管是思想上还是模型本身都比较简单，因此我们希望找到更加复杂的模型来学习词语之间的关系，甚至学习语义，由此我们便想到了神经网络。

Neural Network & max-margin loss

NN

相比于softmax的线性决策，NN的非线性拟合会学习词和词之间的interaction。

仍以 museums in Paris are amazing 为例,在此之前，当 $in$ 出现时，它的下一个词大概率会是一个地名，但是现在，我们可以通过 NN 学习到 things and patterns ，就是说，如果 $in$ 出现在窗口第二词的位置上，当且仅当第一个词是 $museum$ 时， $in$ 后面的词是地名的概率才会增大。

一个简单的网络：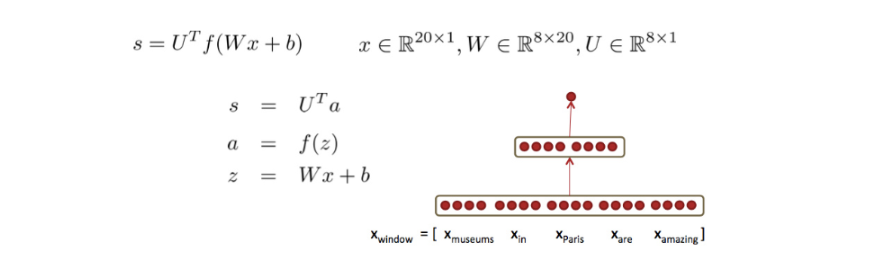

这种红点图经常在论文里看到，大致代表单元数；中间的空格分隔开一组神经元，比如隐藏层单元数为2×4。

U 是隐藏层到class的权值矩阵

$\alpha$ 是激活函数

max-margin

怎么设计目标函数呢，记$s_c$代表误分类样本的得分，$s$表示正确分类样本的得分。则朴素的思路是最大化$(s−s_c)$ 或最小化 $(s_c−s)$。但有种方法只计算$ s_c>s⇒(s_c−s)>0$ 时的错误，也就是说我们只要求正确分类的得分高于错误分类的得分即可，并不要求错误分类的得分多么多么小。这得到间隔最大化目标函数:

$min(J)=max(s_c-s,0)$

但上述目标函数要求太低，风险太大了，没有留出足够的“缓冲区域”。可以指定该间隔的宽度 $s−s_c< \delta$ ，得到：

$min(J)=max(s_c-s + \delta,0)$

可以令 $\delta = 1$

在这个分类问题中，这两个得分的计算方式为：$s_c=U^Tf(Wxc+b)$ 和 $s=U^Tf(Wx+b)$；通常通过负采样算法得到负例。

另外，这个目标函数的好处是，随着训练的进行，可以忽略越来越多的实例，而只专注于那些难分类的实例。

参考资料

nltk-ner