这节课从传统的、基于计数的全局方法出发,过渡到高级的Glove,并介绍了词向量的调参与评测方法
词幂律分布,log之后是线性的
复习:word2vec(skip-gram)
- 遍历整个语料库中的每个词
- 预测每个词的上下文
- 然后在每个窗口(最多有2m+1个词)中做SGD,
word2vec 的 Q
- 整个矩阵都需要更新吗?
- 所有词表中的词都需要进行计算吗?
- 只能在局部上下文窗口训练模型吗?
word2vec 的 A
- 每个窗口相对于整个字典D来说是稀疏的,所以求导也是稀疏的。
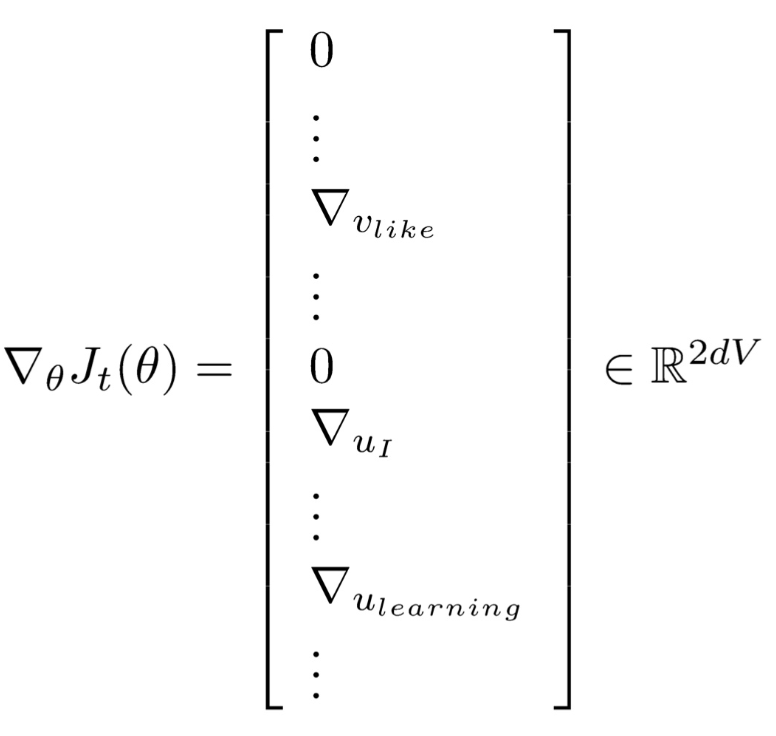
而最终需要去和正确答案比对的,只是这些窗口中出现的词,所以每次更新的也只是W矩阵中的少数列,
- 此外,词表V的量级非常大,以至于下式的分母很难计算。所以提出了negative sampling的方法,这是一种采样子集简化运算的方法。具体做法是,对每个正例(中央词语及上下文中的一个词语)采样几个负例(中央词语和其他随机词语),训练一个二分类器。
- 目标函数是
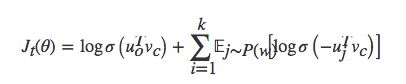
即对于每一个窗口进行k次采样,其中负采样算法的基本思路是对于长度为1的线段,根据词语的词频将其公平地分配给每个词语。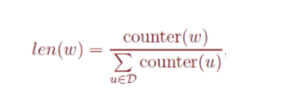
也就是满足“保证频次越高的样本越容易被采样出来”
接下来只要生成一个0-1之间的随机数,看看落到哪个区间,就能采样到该区间对应的单词了,很公平。
为了快速找到小数对应的区间,word2vec用的是一种查表的方式,将上述线段标上M个“刻度”,刻度之间的间隔是相等的,即1/M: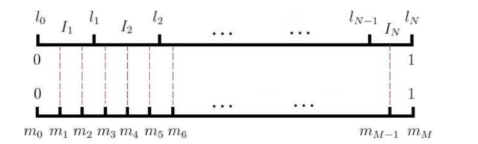
这样就不生成0-1之间的随机数了,只要生成0-M之间的整数,去这个刻度尺上一查就能抽中一个单词了。
在word2vec中,该“刻度尺”对应着table数组。具体实现时,对词频取了0.75次幂:
这个幂实际上是一种“平滑”策略,能够让低频词多一些出场机会,高频词贡献一些出场机会。
- 在word2vec模型提出不久,Jeffrey Pennington等人认为虽然skip-gram模型在计算近义词方面比较出色,但它们只是在局部上下文窗口训练模型,并且它很少使用语料中的一些统计信息,因此Jeffrey Pennington等人又提出了一个新型模型GloVe。
Glove 模型
- 参数说明
(1)词-词共现计数矩阵可以表示为 $X$
(2) 单词 j 在单词 i 中上下文的次数 $X_{ij}$
(3) 表示任何词出现在单词i上下文中的次数表示为 $X_{i}=\sum_kX_{ik}$
(4) 单词j出现在单词i上下文中的比率 可表示为 $P_{ij}$ ,即(2)/(3)
举个例子:说明是怎样从共现概率中抽取确定的意思,其实也就是说,和哪个上下文单词在一起的多,那么这个单词与这个上下文单词在一起要比与其他词在一起意义要大。例如$i=ice$, $j=steam$,假设有共现词$k$,但是$k$与$ice$的联系要比与$steam$的联系强,也就是说单词$k$与$ice$出现的概率比与$steam$出现的概率大,比如说$k=solid$,那么认为 $P_{ik} \over P_{jk}$ 会很大。相似地,如果单词$k$与$steam$的联系比与$ice$的联系强,例如$k=gas$,那么$P_{ik} \over P_{jk}$ 的比率会很小,对于其他的单词$k$如$water, fashion$与$ice,steam$联系都强或都不强的话,则 $P_{ik} \over P_{jk}$ 的比率会接近1。那么这个比率就能区别相关词 $(solid, gas)$ 和不相关词 $(water, fashion)$ ,并且也能区别这两个相关的词 $(solid, gas)$ 。那么得到的向量可能为 $ice-steam=solid-gas$ ,这与word2vec相似。
模型训练
(1)对于词向量的学习开始于共现概率的比率 $P_{ik} \over P_{jk}$,最一般的形式为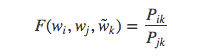
其中$w$是词向量, $\tilde{w}$ 是上下文单词向量
由于向量空间是线性的,所以可以把两个向量表示为向量的差,则可以把上式写成:
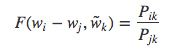
由于等式右边是一个标量,则等式左边参数可以表示为点积形式:
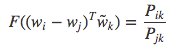
由于一个单词与其上下文单词的区别是任意的,它们两个的角色是可以互换的,所以单词 $w$ 可与 $\tilde{w}$ 互换,并且矩阵 $X$ 与 $X^{T}$ 也可以互换,但对于最终结果都是不变的。然后把原始概率用 $F$ 函数表示,则:
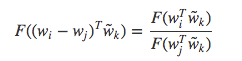
其中, $F(w_i^{T}\tilde{w}) = P_{ik}$, $P_{ik}$ = $X_{ik} \over X_{i}$.当 $F=exp$ 时,上式为:
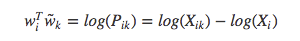
因为多存在了一个 $log(X_i)$,所以这个式子不具有对称性,我们注意到,$log(X_i)$ 与 k无关,所以把这一项放到了对 $w_i$ 偏置的 $b_i$中,最后再加上对 $\tilde{w}_{k}$ 的偏置 $\tilde{b}_{k}$,则:
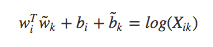
这是$F(w_i, w_j, \tilde{w}_k)=P_{ik}/P_{jk}$的简化,并具有对称性。当 $X_{ik}$ 接近于0时对数是发散的,所以可以把 $log(X_{ik})$ 转化为 $log(1+X_{ik})$
该模型的一个主要缺点为它认为所有的共现词权重相等,即使很少出现或没有出现的词,所以为了克服这一缺点,使用了加权最小二乘回归模型:
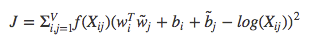
不同模型的对比
Omer Levy等人对基于计数的方法和基于embedding的方法做了对比,发现它们之间并没有非常大的差距,在不同的场景各个模型发挥不同的作用,它们之间并没有谁一定优于谁,相比于算法而言,增加语料量,进行预处理以及超参数的调整显得非常重要。特别指出,基于negtive sampling的skip-gram模型可以作为一个基准,尽管对不同的任务它可能不是最好的,但是它训练快,占用内存和磁盘空间少。