有了 原理篇 做基础,这次来进行一个简单的实战,从最简单的上下文只有一个词的情形入手, 利用朴素softmax和用梯度下降,多轮迭代进行模型训练。
模型结构
首先先看简化版入手: 输入输出都只有一个词,如下图示:
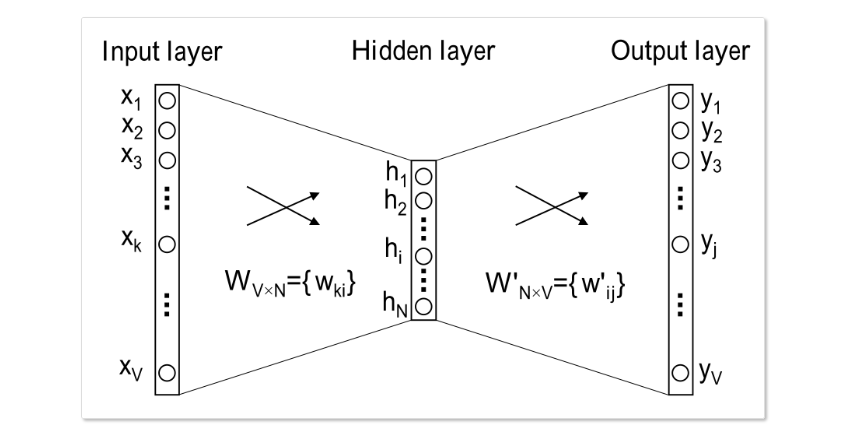
首先说明符号:
- $x$: 输入是一个词,这个词用 one-hot 编码方式表示成的向量,维度等于词表长度 $V$, 只有输入词编号位置是 1,其他都是 0;
- $V$: 词汇表长度;
- $N$: 隐层神经元个数, 同时也是词向量维度;
- $W \in R^{V \times N}$, 输入层到隐层的权重矩阵, 其实就是词向量矩阵,其中每一行代表一个词的词向量(称之为输入向量,也是 word2vec 的最终产出);
- $W’ \in R^{N \times V}$,隐层到输出层的权重矩阵, 其中每一列也可以看作额外的一种词向量;
然后,因为是神经网络,所以中间有一个隐藏层 $h$,和通常的神经网络(深度神经网络更是如此)不同,这个隐藏层没有非线性激活函数。$h$ 有 $N$ 个神经元,这个 $N$ 就是最终给每个词学习到的向量长度,是一个超参数,所谓超参数就是开始计算只要需要人指定的参数。隐藏层的输出就是 $H_{N\times 1}=W_{V \times N}^{T} \times X_{V \times 1}$
- $y$: 每个词的概率.其实是一个多项分布.
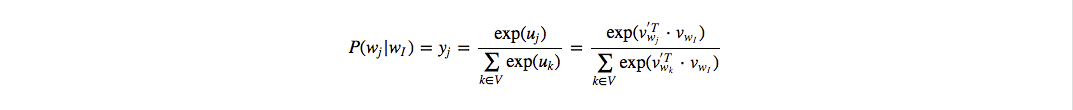
其中 $v_w$ 与$v_{w}$ 都称为词 $w$ 的词向量,一般使用前者作为词向量,而非后者。至此前向过程完成,就是给定一个词作为输入,来预测它的上下文词,还是比较简单的,属于简化版的神经语言模型。
训练及更新
首先明确训练数据的格式,对于一个训练样本($w_I$, $w_O$),输入是词 $w_I$ 的 one-hot 的维度为 $V$ 的向量 $x$,模型预测的输出同样也是一个维度为$V$的向量y, 同时真实值 $w_O$ 也是用one-hot表示,记为 $t=[0,0,0,…1,0,0]$,其中假设 $t_{j^∗}=1$, 也就是说 $j^∗$ 是真实单词在词汇表中的下标,那么根据最大似然或者上面的语言模型,目标函数可以定义如下: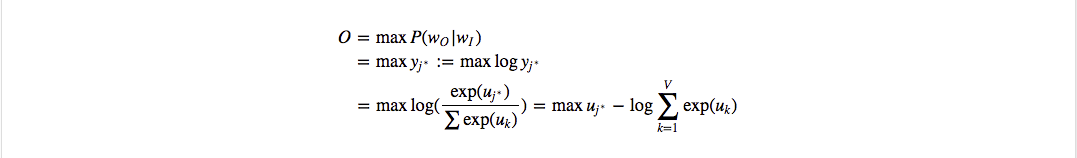
一般我们习惯于最小化损失函数,因此定义损失函数: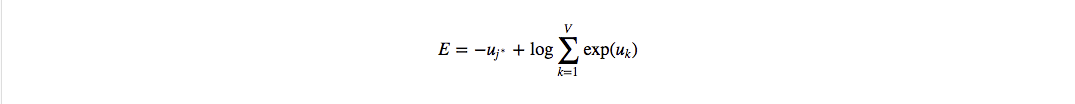
然后结合反向传播一层层求梯度,使用梯度下降来更新参数。
更新输出矩阵
先求隐层到输出层的向量矩阵W’的梯度: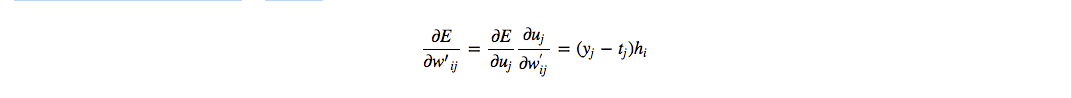
这里面的 $y_j$和 $t_j$ 分别是预测和真实值的第$j$项,$h_i$是隐层的第 $i$ 项。
因此梯度下降更新公式为: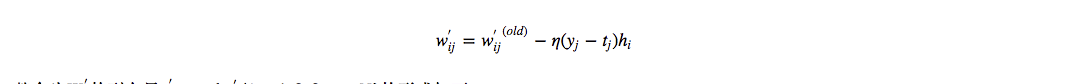
整合为W′的列向量 $v^{‘}_{w_j} ={w^{‘}_{ij}|i=1,2,3,…,N}$ 的形式如下: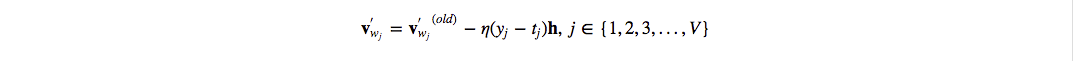
也就是说对每个训练样本都需要做一次复杂度为 $V$ 的操作去更新 $W^{‘}$
更新输入矩阵
接着考虑隐层 $h$ 的更新,其实也是输入层到隐层的矩阵 $W$ 的更新,继续反向传播,跟神经网络的相同, 输出层的 $V$ 个神经元都会影响$h_i$: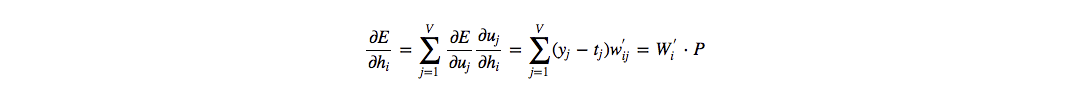
其中$W^{‘}_i$是 $W′$ 的第i行, 这里为了方便书写,令 $P$={$y_j−t_j|j=1,2,3,..,V$}, 因此整合成整个隐层的向量$h$: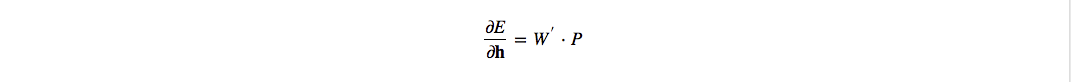
得到一个$N$维的向量,上面已经介绍过,$h$ 就是词向量矩阵$W$的一行: $W^T X = v_{w_I}^T$.
如果对这一段的推导印象模糊,可以参考反向传播与梯度计算
对应的矩阵运算表示就是:
又因为
综合起来,输入矩阵的梯度计算就是:
得到梯度后,每次就可以按照如下公式迭代更新 $W_{V\times N}$:
训练过程
迭代之前,随机初始化两个矩阵,然后每轮迭代过程就是三步:
- 计算输出概率;
- 计算输出矩阵的梯度,更新输出矩阵参数;
- 计算输入矩阵的梯度,更新输入矩阵参数。
我们把原始语料库拆解成词对: (左边词,当前词) (右边词,当前词) 然后构造成训练样本。
python 实现
1 | # coding: utf-8 |
简单测试
构造了一个简单的语料库
1 | 吃 米饭 喝 啤酒 |
训练模型:
1 | python word2vec-simple.py |
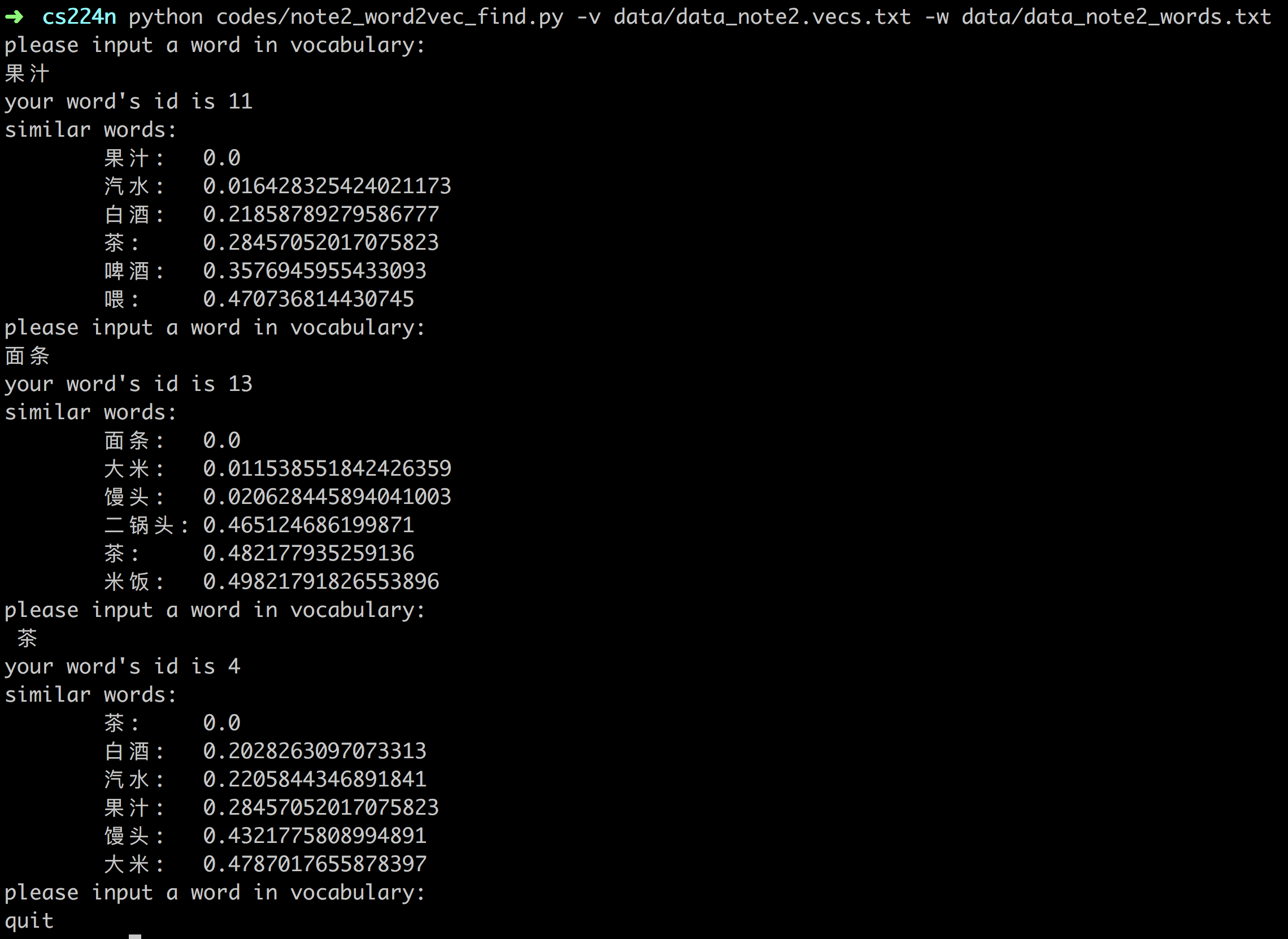
写一个程序用来查找相似词:
# -*- coding: utf-8 -*-
import numpy as np
from scipy.spatial.distance import cosine
import argparse
import math
import sys
import operator
class FeatureIndex():
def __init__(self):
self.word_to_index = {}
self.index_to_word = {}
def read_word_idx(self, fn):
with open(fn, 'r') as fr:
lines = fr.readlines()
for line in lines:
line = line.strip().split("\t")
self.index_to_word[line[1]] = line[0]
self.word_to_index[line[0]] = line[1]
class VectorIndex:
def __init__(self):
self.idx_vec_pair = {}
def read_vectors(self, vectorfile):
with open(vectorfile) as vectorfile_input:
wordid = 0
for line in vectorfile_input:
vector = [float(s) for s in line.strip().split()]
self.idx_vec_pair[str(wordid)] = vector
wordid += 1
def get_topK_similar(self, wordid, k):
"""与查找词最近的k个词"""
vec_input = self.idx_vec_pair[str(wordid)]
scores = {}
for wordid in self.idx_vec_pair:
vec_curr = self.idx_vec_pair[wordid]
score = cosine(vec_input, vec_curr)
scores[wordid] = score
scores = sorted(scores.items(), key=operator.itemgetter(1))
k = min(k+1, len(scores))
return scores[:k]
def main(vectorfile, vocabularyfile):
vocabulary = FeatureIndex()
vocabulary.read_word_idx(vocabularyfile)
vector_index = VectorIndex()
vector_index.read_vectors(vectorfile)
while True:
print("please input a word in vocabulary:")
line = sys.stdin.readline()
line = line.strip()
if line == 'exit' or line == 'quit':
break
wordid = vocabulary.word_to_index[line]
if wordid is None:
print('sorry, the word you input is not in our corpus.')
else:
print("your word's id is %s" % wordid)
result = vector_index.get_topK_similar(wordid, 5)
print("similar words:")
similar_words = [vocabulary.index_to_word[r[0]] for r in result]
for i in range(len(similar_words)):
print("\t%s:\t%s" % (similar_words[i], result[i][1]))
if __name__ == '__main__':
parser = argparse.ArgumentParser(description = 'query similar words from vectors')
parser.add_argument('-v', '--vector', help = """vector file from word2vec""")
parser.add_argument('-w', '--words', help = """all words and its id(vocabulary)""")
args = vars(parser.parse_args())
if args['vector'] is None or args['words'] is None:
parser.print_help()
exit()
main(args['vector'], args['words'])